PROGRAM LINEAR

Nama: Diena Naila Amalia

Kelas: XI IPS 1

Program Linear

A. Pertidaksamaan Linear Dua Variabel

Konsep persamaan dan sistem persamaan linear dua variabel sudah kamu pelajari. Prinsip yang ada pada sistem persamaan juga kita gunakan untuk menyelesaikan pertidaksamaan atau sistem pertidaksamaan linear dua variabel.

Prinsip yang dimaksud adalah menentukan nilai variabel yang memenuhi sistem pertidaksamaan linear tersebut.

Definisi

Pertidaksamaan linear dua variabel adalah pertidaksamaan yang berbentuk

ax + by + c < 0

ax + by + c ≤ 0

ax + by + c > 0

ax + by + c ≥ 0

dengan:

a, b : koefisien (a ≠ 0, b ≠ 0, a,b ∈ R)

c : konstanta (c ∈ R)

x, y : variabel (x, y ∈ R)

B. Daerah Bersih dan Daerah Kotor

Gambar daerah bersih dan daerah kotor dari pertidaksamaan 3x + 2y ≤ 12, 5x + 3y < 19, x ≥ 0, y > 0

PENYELESAIAN:

• 3x + 2y ≤ 12

 x = 0

3.0 + 2y = 12

         2y = 12

           y = 6

3x + 2.0 = 12

         3x = 12

           x = 4

• 5x + 3y < 19

  y = 0

 5x + 3.0 = 19

          5x = 19

            x = 3,8

 5.0 + 3y = 19

          3y = 19

            y = 6,3

DAERAH PENYELESAIAN

daerah penyelesaian x ≥ 0

daerah penyelesaian y > 0

 DAERAH ARSIRAN

gambar daerah kotor

gambar daerah bersih

Contoh Soal

Tentukan himpunan penyelesaian dan gambarkan grafik untuk setiap pertidaksamaan di bawah ini.

 –2x + y > 5, untuk x dan y semua bilangan real

Alternatif Penyelesaian

Dengan menguji nilai-nilai x dan y yang memenuhi – 2x + y > 5 , maka dapat ditemukan banyak pasangan x dan y yang memenuhi pertidaksamaan.

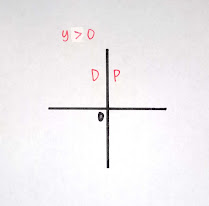
Ilustrasi himpunan penyelesaian, jika dikaji secara geometris disajikan pada gambar berikut.

Dari gambar diperoleh bahwa terdapat titik yang tak hingga banyaknya (daerah yang tidak diarsir) yang memenuhi –2x + y > 5.

Kali ini, melalui grafik, kita dapat memilih sembarang titik, misalnya titik (–5, 0), sedemikian sehingga –2(–5) + 0 = 10 > 5 adalah pernyataan benar.

Program Linear

Definisi

Masalah program linear dua variabel adalah menentukan nilai x1, x2 yang memaksimumkan (atau meminimumkan) fungsi tujuan,

Z(x1, x2) = C1x1 + C2x2

dengan kendala:

Contoh

Gambarkan daerah penyelesaian sistem pertidaksamaan berikut ini.

Alternatif Penyelesaian:

Untuk menggambarkan daerah penyelesaian setiap pertidaksamaan pada sistem di atas, dapat dimulai dengan menggambar satu per satu pertidaksamaan yang diketahui. Tentu, semua daerah penyelesaian tersebut nanti harus disajikan dalam satu bidang koordinat kartesius.

a. Daerah penyelesaian untuk sistem pertidaksamaan (a) di atas, adalah sebagai berikut

b. Daerah penyelesaian untuk sistem pertidaksamaan (b) di atas, adalah sebagai berikut:

Jadi, tidak ada nilai x dan y yang memenuhi sistem pertidaksamaan b). Hal ini, perlu dicatat, bahwa tidak semua masalah memiliki penyelesaian.

C. Masalah Konstektual Yang Berhubungan dengan Program Linear

1. Ada seorang pedagang buah naga sedang memanen hasil kebunnya. Dia menyewa 30 kendaraan jenis truk dan colt dengan total muatan sebanyak 300 karung. Setiap truk hanya mampu menampung 15 karung dan colt hanya mampu mengangkut 10 karung. Tentukanlah bentuk model matematikanya.

Pembahasan

Dalam mengerjakan soal cerita seperti ini, Kita dapat melakukan pemisalan pada truk dan colt. Kita anggap truk sebagai fungsi x dan colt sebagai fungsi y. Selain itu, banyak karung yang di tampung adalah 300 karung dengan masing-masing per truk mampu menampung 15 karung dan colt 10 karung. Sehingga kita bisa menuliskan model matematikanya seperti di bawah ini.

Fungsi banyak karung = 15x + 10y = 300

Fungsi banyak karung = 3x + 2y = 60

Fungsi kuantitas = x + y = 30

Sehingga model matematika soal tersebut adalah F(kuantitas): x + y = 30 dan F(banyak karung): 3x + 2y = 60.

2. Lendra sedang berbelanja ke pasar. Dia membeli beberapa buah rambutan dan pepaya. Jumlah yang dibeli paling sedikit 20 buah di mana buah rambutan maksimal sebanyak 12 buah. Harga rambutan per buah adalah 5 ribu dan pepaya adalah 2 ribu. Ia memiliki uang 40 ribu. Jika Lendra membeli a rambutan dan b pepaya, tentukan bentuk model matematikanya

Pembahasan

Seperti soal sebelumnya, kita melakukan pemisalan untuk pembelian dan jumlah buah di mana rambutan sebagai fungsi x dan pepaya sebagai fungsi y.

Fungsi pembelian: 5000x + 2000y = 40000

Fungsi pembelian: 5x + 2y = 40

Fungsi jumlah buah: x + y ≥ 20

Fungsi maksimal rambutan: x ≤ 12

Ini bentuk model matematika untuk semua informasi dalam soal tersebut.

3. Diketahui sebuah persamaan x + y = 10 dan diberikan sebuah fungsi seperti di bawah ini

{(x,y)| x ≥ 0; y ≥ 0; 2x + 3y ≤ 8; 3x + 2y ≤ a}

Tentukan nilai a pada fungsi di atas sehingga nilai maksimum x + y = 10

Pembahasan

Pertama, kita harus menuliskan semua fungsi yang ada secara benar seperti contoh di bawah ini.

x ≥ 0

y ≥ 0

2x + 3y ≤ 8

3x + 2y ≤ a

Kemudian, lakukan penjumlahan dari dua fungsi di atas.

2x + 3y ≤ 8

3x + 2y ≤ a    +

5x + 5y ≤ 8 + a

5 (x + y) ≤ 8 + a

5 (10) ≤ 8 + a

50 – 8 ≤ a

42 ≤ a

Sehingga, nilai a ≥ 42 untuk mendapatkan nilai maksimum x + y = 10.

4. Punto merupakan seorang pedagang memiliki modal Rp. 1.000.000 untuk membeli anggur dan ketan beras. Harga beli tiap kg anggur adalah Rp. 4000 dan ketan besar adalah Rp. 1600. Gudang Punto hanya bisa menampung 400 kg. Tentukan jumlah anggur dan ketan beras maksimum.

Pembahasan

Seperti soal-soal sebelumnya, kita dapat melakukan pemisalan pada soal tersebut di mana anggur sebagai fungsi x dan ketan besar sebagai fungsi y. Maka, kita bisa menulis bentuk pertidaksamaannya sebagai berikut.

Fungsi kapasitas: x + y ≤ 400

Fungsi modal: 4000x + 1600y ≤ 1.000.000 disederhanakan menjadi 5x + 2y ≤ 1250

x ≤ 0 ; y ≤ 0

Dari persamaan tersebut, kita dapat membentuk sebuah diagram sesuai dengan nilai maksimum pada tiap persamaan. Kita bisa memasukkan nilai 0 dan 400 dalam tiap persamaan sehingga bisa diketahui titik ekstremnya.

• Titik 1 (0,400) merupakan titik ekstrem namun tidak terdapat fungsi anggur
• Titik 3 (400,0) merupakan titik ekstrem namun tidak terdapat fungsi beras ketan
• Titik 2 ( xb, yb ) menggunakan eliminasi kedua fungsi di atas.

5x + 2y ≤ 1250

x + y ≤ 400 |x2   –

5x + 2y ≤ 1250

2x + 2y ≤ 800    –

3x ≤ 450

Sehingga nilai x adalah 150. Total anggur dan beras ketan adalah 400, sedangkan jumlah angggur adalah 150, maka jumlah beras ketan adalah 250.

5. Jika diberikan sebuah fungsi f(x,y) = 4x + 5y pada grafik di bawah ini. Tentukan garis maksimum fungsi tersebut

Pembahasan

Pertama, kita harus melihat titik-titik ekstrem pada gambar di atas. Sehingga di temukan titik ekstremnya adalah B(3,6), C(8,2), dan D(8,0).

Kemudian, kita masukkan titik ekstrem ini ke dalam persamaan f(x,y) = 4x + 5y.

Nilai terbesar merupakan titik maksimumnya. Berdasarkan perhitungan, titik maksimum melintasi garis BC. Sehingga bisa disimpulkan bahwa BC adalah garis maksimum.

Daftar Pustaka:

https://wirahadie.com/materi-matematika-kelas-11-bab-2/

https://rumuspintar.com/program-linear/