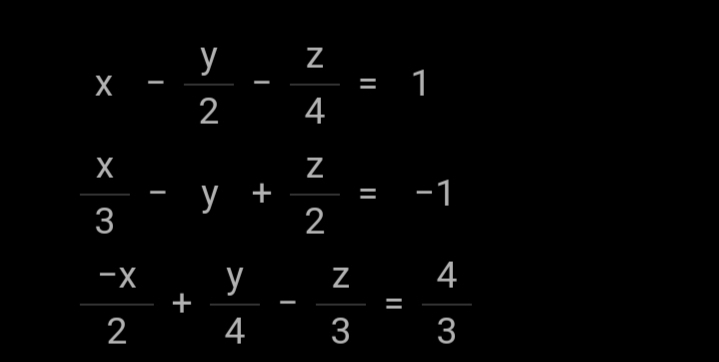Soal Cerita SPLTV dalam kehidupan sehari-hari

Diena Naila Amalia

08/ X IPS 3

Soal Cerita SPLTV dalam kehidupan sehari-hari

No 1. 

Dua tahun yang lalu seorang laki-laki umurnya 6 kali umur anaknya. 18 tahun kemudian umurnya akan menjadi dua kali umur anaknya. Carilah umut mereka sekarang!

Pembahasan:

Misalkan umur ayah sekarang x tahun dan umur anaknya y yahun, maka:

x - 2 = 6(y - 2)

⇔ x - 2 = 6y - 12

⇔ x - 6y = -12 + 2

⇔ x - 6y = -10 ..........(1)

18 tahun kemudian:

x + 18 = 2(y + 18)

⇔ x + 18 = 2y + 36

⇔ x - 2y = 36 - 18

⇔ x - 2y = 18 ...........(2)

Eliminasi persamaan (1) dan (2) diperoleh:

x - 6y = -10

x - 2y = 18 -

⇔ -4y = -28

⇔ y = -28/-4

⇔ y = 7

Subtitusi nilai y = 7 ke persamaan (1) diperoleh:

x - 2y = 18

⇔ x - 2(7) = 18

⇔ x - 14 = 18

⇔ x = 18 + 14

⇔ x = 32

Jadi, sekarang umur ayah 32 tahun dan anaknya berumur 7 tahun.

No 2. 

Raisa dan Sekar secara bersamaan membutuhkan waktu 12 menit untuk mencetak foto. Sekar dan Aira membutuhkan 15 menit untuk menyelesaikan pekerjaan yg sama . Sedangkan Raisa dan Aira membutuhkan waktu 20 menit untuk mencetak foto. Berapa waktu yg di perlukan oleh Raisa, Sekar, Aira untuk mencetak foto yang sama secara bersama-sama adalah ... menit.

A. 5

B. 8

C. 10

D. 11

E. 13

Pembahasan :

Bagian pekerjaan yang bisa diselesaikan dalam 1 menit secara sendiri-sendiri

Raisa = 1/x bagian

Sekar = 1/y bagian

Aira = 1/z bagian

Kita buat persamaan dari penyataan diatas

1/x + 1/y = 1/12 ... pers I

1/y + 1/z = 1/15 ... pers II

1/x + 1/z = 1/20 ... pers III

Jumlahkan persamaan I, II, dan III

 1/x + 1/y = 1/12

          1/y + 1/z = 1/15

 1/x + 1/z = 1/20

------------------------------ +

2(1/x) + 2(1/y) + 2(1/z) = 1/12 + 1/15 + 1/20

       2 (1/x + 1/y + 1/z) = 5/60 + 4/60 + 3/60

       2 (1/x + 1/y + 1/z) = 12 / 60

            1/x + 1/y + 1/z = 12/60 × 1/2

             1/x + 1/y + 1/z = 6 / 60

bersama-sama mereka bertiga mengerjakan mencetak foto

1/n = 1/x + 1/y + 1/z

1/n = 6/60

   n = 60/6

   n = 10

no 3

Di dalam dompet Laras terdapat 25 lembar uang lima ribu rupiah dan 10 ribu rupiah. Jumlah uang itu adalah Rp200.000,00. Berapa jumlah uang itu masng-masing?

Pembahasan:

Misalkan banyaknya uang sepuluh ribu rupiah adalah x lembar dan uang lima ribu rupiah adalah y lembar, maka:

Banyak uang Laras 25 lembar

x + y = 25 ..........(1)

Jumlah uang Laras Rp200.000,00

10.000x + 5.000y = 200.000

2x + y = 40 .......(2)

Eliminasi persamaan (1) dan (2) diperoleh:

x + y = 25

2x + y = 40

-x = -15

x = 15

Subtitusi nilai x = 15 ke persamaan (1):

x + y = 25

15 + y = 25

y = 25 - 15

y = 10

Jadi:

Jumlah uang sepuluh ribu rupiah = 15 x Rp10.000,00 = Rp150.000,00

Jumlah uang lima ribu rupiah = 10 x Rp5.000,00 = Rp50.000,00

no 4

Misalkan panjang dan lebar tanah itu masing-masing adalah x meter dan y meter.

Keliling = (2 . panjang) + (2 . lebar)

48 = 2x + 2y

24 = x + y atau

x + y =24 .........(1)

Panjangnya lebih 6 meter dari lebarnya

panjang = lebar + 6

x = y + 6 ........(2)

Subtitusi persamaan (2) ke persamaan (1):

x + y = 24

(y + 6) + y = 24

       2y + 6 = 24

             2y = 24 - 6

             2y = 18

               y = 18/2

               y = 9

Subtitusi nilai y = 9 ke persamaan (2):

x = y + 6

x = 9 + 6

x = 15

Jadi, ukuran tanah itu adalah 15meter x 9meter.

https://www.ruangsoal.id/2018/07/soal-dan-pembahasan-penerapan-spldv.html?m=1

Sistem persamaan linear tiga variabel atau disingkat SPLTV

Diena Naila Amalia

08 / X IPS 3

Sistem persamaan linear tiga variabel atau disingkat SPLTV adalah suatu persamaan matematika yang terdiri atas 3 persamaan linear berderajat satu yang masing-masing persamaan bervariabel tiga (misal x, y dan z). Dengan demikian, bentuk umum dari Sistem Persamaan Linear Tiga Variabel dalam x, y, dan z dapat ditulis sebagai berikut:

ax + by + cz = d

atau

a1x + b1y + c1z = d1

ex + fy + gz = h

a2x + b2y + c2z = d2

ix + jy + kz = l

a3x + b3y + c3z = d3

Dengan a, b, c, d, e, f, g, h, i, j, k, dan l atau a1, b1, c1, d1, a2, b2, c2, d2, a3, b3, c3, dan d3 merupakan bilangan-bilangan real.

Keterangan:

a, e, I, a1, a2, a3 = koefisien dari x

b, f, j, b1, b2, b3 = koefisien dari y

c, g, k, c1, c2, c3 = koefisien dari z

d, h, i, d1, d2, d3 = konstanta

x, y, z = variabel atau peubah

cara menentukan himpunan penyelesaian SPLTV berbentuk pecahan

Namun dalam soal-soal matematika yang berhubungan dengan sistem persamaan linear tiga variabel terkadang kita menemui SPLTV yang berbentuk pecahan seperti sistem persamaan linear berikut ini.

Lalu bagaimana menentukan himpunan penyelesaian SPLTV yang berbentuk pecahan tersebut? Caranya sangat mudah sekali, yaitu kita hanya perlu mengubah SPLTV pecahan menjadi bentuk baku atau bentuk umum seperti yang telah disebutkan di awal artikel. Setelah bentuk baku diperoleh, selanjutnya kita selesaiakan dengan menggunakan salah satu dari metode-metode berikut ini.

■ Metode subtitusi

■ Metode eliminasi

■ Metode gabungan atau campuran

■ Metode determinan

■ Metode invers matriks

Sebagai contoh, kita akan menentukan himpunan penyelesaian dari sistem persamaan linear tiga variabel yang berbentuk pecahan berikut ini.

Langkah-langkahnya adalah sebagai berikut.

■ Ubah persamaan yang memuat pecahan menjadi bentuk baku. Caranya adalah dengan mengalikan kedua ruas dengan KPK dari penyebut-penyebut pecahannya yaitu sebagai berikut.

Persamaan 1

KPK dari 1, 2 dan 4 adalah 4, oleh karena itu, agar menjadi bentuk baku, kita kalikan kedua ruas dengan angka 4 sehingga hasilnya adalah sebagai berikut.

4x – 2y – z = 4

Persamaan 2

KPK dari 3, 1, dan 2 adalah 6 oleh karena itu, agar menjadi bentuk baku, kita kalikan kedua ruas dengan angka 6 sehingga hasilnya adalah sebagai berikut.

2x – 6y + 3z = −6

Persamaan 3

KPK dari 2, 4 dan 3 adalah 12 oleh karena itu, agar menjadi bentuk baku, kita kalikan kedua ruas dengan angka 12 sehingga hasilnya adalah sebagai berikut.

−6x + 3y – 4z = 16

Dengan demikian, bentuk baku dari sistem persamaan linear tiga variabel bentuk pecahan di atas adalah sebagai berikut.

4x – 2y – z = 4 ……………….. Pers. (1)

2x – 6y + 3z = −6 ………….. Pers. (2)

−6x + 3y – 4z = 16 .……….. Pers. (3)

 

Baca Juga:

Kumpulan Contoh Soal SPLDV, SPLTV, SPLK, SPKK dan Jawabannya

Kumpulan Contoh Soal dan Jawaban SPLTV (Sistem Persamaan Linear Tiga Variabel)

5 Macam Metode Menentukan Penyelesaian SPLTV + Contoh Soal dan Pembahasan Bagian 3

 

■ Setelah bentuk SPLTV kita dapatkan, langkah selanjutnya adalah menentukan himpunan penyelesaian dari SPLTV tersebut dengan menggunakan salah satu dari 5 metode penyelesaian SPLTV di atas. Misalkan kita akan menggunakan metode campuran (eliminasi + subtitusi), sehingga penyelesaiannya adalah sebagai berikut.

#1 Metode Eliminasi (SPLTV)

Langkah pertama, kita tentukan variabel mana yang akan kita eliminasi terlebih dahulu. Untuk mempermudah, lihat variabel yang paling sederhana. Dari ketiga SPLTV di atas, variabel yang paling sederhana adalah y sehingga kita akan mengeliminasi y dulu. Untuk menghilangkan peubah z, maka kita harus menyamakan koefisien masing-masing y dari ketiga persamaan. Perhatikan cara berikut.

4x – 2y – z = 4 → koefisien y = –2

2x – 6y + 3z = −6 → koefisien y = –6

−6x + 3y – 4z = 16 → koefisien y = 3

Agar ketiga koefisien y sama (abaikan tanda), maka kita kalikan persamaan pertama dengan 3, persamaan kedua dengan 1, dan persamaan ketiga dengan 2. Sehingga hasilnya adalah sebagai berikut.

4x – 2y – z

=

4

|× 3|

→

12x – 6y – 3z

=

12

2x – 6y + 3z

=

−6

|× 1|

→

2x – 6y + 3z

=

−6

−6x + 3y – 4z

=

16

|× 2|

→

−12x + 6y – 8z

=

32

 

Setelah koefisien y ketiga persamaan sudah sama, maka langsung saja kita kurangkan atau jumlahkan persamaan pertama dengan persamaan kedua dan persamaan kedua dengan persamaan ketiga sedemikian rupa hingga variabel y hilang. Prosesnya seperti di bawah ini.

● Dari persamaan pertama dan kedua:

12x – 6y – 3z

=

12

2x – 6y + 3z

=

−6

−

10x − 6z

=

18

● Dari persamaan kedua dan ketiga:

2x – 6y + 3z

=

−6

−12x + 6y – 8z

=

32

+

−10x − 5z

=

26

Dengan demikian, kita peroleh SPLDV sebagai berikut.

10x – 6z = 18

−10x − 5z = 26

#2 Metode Subtitusi (SPLDV)

Dari SPLDV pertama, kita peroleh persamaan x sebagai berikut.

⇒ 10x – 6z = 18

⇒ 10x = 18 + 6z

Lalu kita subtitusikan persamaan y tersebut ke SPLDV kedua sebagai berikut.

⇒ −10x − 5z = 26

⇒ −(18 + 6z) − 5z = 26

⇒ −18 − 6z − 5z = 26

⇒ − 6z − 5z = 26 + 18

⇒ −11z = 44

⇒ z = −4

Kemudian, untuk menentukan nilai x, kita subtitusikan nilai z = −4 ke dalam salah satu SPLDV, misalnya persamaan 10x – 6z = 18 sehingga kita peroleh:

⇒ 10x – 6z = 18

⇒ 10x – 6(−4) = 18

⇒ 10x + 24 = 18

⇒ 10x = 18 – 24

⇒ 10x = –6

⇒ x = –6/10

⇒ x = –3/5

Langkah terakhir yaitu menentukan nilai y. Untuk menentukan nilai y, kita subtitusikan nilai x = –3/5 dan z = x = –4 ke dalam salah satu SPLTV di atas, misalnya persamaan 4x – 2y – z = 4 sehingga kita peroleh:

⇒ 4x – 2y – z = 4

⇒ 4(–3/5) – 2y – (–4) = 4

⇒ –12/5 – 2y + 4 = 4

⇒ –2y = 4 – 4 + 12/5

⇒ –2y = 12/5

⇒ y = –12/10

⇒ y = –6/5

⇒ y = –11/5

Dengan demikian kita peroleh nilai x = –3/5, y = –11/5 dan z = –4  sehingga himpunan penyelesaian SPLTV di atas adalah {(–3/, –11/5, –4)}.

SPLTV bentuk pecahan yang dibahas dalam artikel ini adalah posisi ketiga variabel (x, y, z) sebagai pembilang dalam pecahan. Lalu bagaimana cara menyelesaikan SPLTV bentuk pecahan yang variabelnya dijadikan sebagai penyebut pecahan? Perhatikan contoh SPLTV berikut.

Cara menentukan himpunan penyelesaian SPLTV pecahan dengan model seperti di atas dapat kalian jumpai dalam artikel tentang Contoh Soal + Pembahasan SPLTV Bentuk Pecahan.

PERSAMAAN DAN PERTIDAKSAMAAN NILAI MUTLAK

Diena Naila Amalia

08/X IPS 3

pengertian

Pertidaksamaan adalah kalimat terbuka yang mneggunakan tanda ketidaksamaan (<, >, , ) dan mengandung variakel. Secara umum pertidaksamaan merupakan cara untuk menyatakan suatu selang atau interval. Tanda “<” dan “>” menyatakan selang terbuka dan pada garis bilangan yang digambarkan dengan noktah kosong( ).

Pertidaksamaan nilai mutlak merupakan jenis pertidaksamaan yang mengandungnilai mutlak. Nilai mutlak menghitung suatu angka dari 0—misal, x. mengukur jarak x dari nol.

Persamaan nilai mutlak merupakan sebuah persamaan yang selalu bernilai positif.Pertidaksamaan nilai mutlak adalah sebuah perbandingan ukuran dua objek atau lebih yang selalu bernilai positif.

Rumus Pertidaksamaan Nilai Mutlak

Nilai mutlak suatu bilangan real x adalah jarak antara bilangan itu dengan nol pada garis bilangan. Dan digambarkan dengan x│. Secara formal nilai mutlak didefinisikan sebagai berikut :

Rumus Pertidaksamaan

Pengantar Nilai Mutlak

Fungsi nilai mutlak merupakan fungsi yang kontinu. Jika kita gambarkan dalam bentuk grafik, gambar nilai mutlak membentuk garis lurus, seperti huruf v pada interval tertentu.

Grafik yang dihasilkan memiliki satu buah titik puncak dan garisnya simetris, antara ruas kanan dan kiri.

Perhatikan gambar grafik nilai mutlak yang diberikan seperti gambar di bawah ini.

Grafik Nilai Mutlak

Dan seperti yang terlihat pada kasusu di atas bahwa nilai fungsi mutlak selalu positif (di atas sumbu x).

Sifat-Sifat Pertidaksamaan Nilai Mutlak

Untuk mengambil nilai mutlak dari persamaan nilai mutlak mudah. Dengan mengikuti 2 aturan penting seperti yang telah dibahas sebelumnya dapat menentukan nilai mutlaknya. Jadi, nilainya akan positif jika fungsi di dalam tanda mutlak lebih dari nol. Dan akan bernilai negatif jika fungsi di dalam tanda mutlak kurang dari nol.

Dalam pertidaksamaan nilai mutlak tidak cukup dengan cara tersebut. Ada beberapa ketidaksamaan aljabar yang ekuivalen dengan ketidaksamaan nilai mutlak. Ataupun dapat disebut saja sebagai sifat pertidaksamaan nilai mutlak.

Sifat inilah yang dapat dipakai untuk menentukan himpunan penyelesaian pada soal-soal pertidaksamaan nilai mutlak yang diberikan.

Sifat-sifat tidak samaan nilai mutlak adalah sebagai berikut :

Sifat-sifat pertidaksamaan nilai mutlak

Dalam menyelesaikan pertidaksamaan nilai mutlak, selain perlu mengetahui sifa-sifat yang telah diberikan di atas, kita juga perlu kemampuan untuk menguasai cara oprasi bentuk aljabar. Cara dasar dalam mengoperasikan suatu bilangan dan variabel.

Soal Pertidaksamaan Nilai Mutlak

Contoh Soal 1

Tentukan interval pada penyelesaian pertidaksamaan berikut ini :

Soal 1

Jawab :

Jawaban Soal 1

Contoh Soal 2

Himpunan penyelesaian pertidaksamaan berikut :

Soal 2

Jawab :

Contoh Soal Persamaan Nilai Mutlak

Contoh Soal 1

Berapa nilai mutlak dari persamaan |10-3|?

Jawab :

|10-3|=|7|=7

Contoh Soal 2

Berapa hasil x untuk persamaannilai mutlak |x-6|=10?

Jawab:

Untuk menyelesaikan persamaan tersebut, terdapat dua kemungkinan hasil bilangan mutlak

|x-6|=10

Solusi pertama:

x-6=10

x=16

solusi kedua:

x – 6= -10

x= -4

Jadi, jawaban untuk persamaan ini yaitu 16 atau (-4)

NILAI MUTLAK

Diena Naila Amalia

08/X IPS 3

PENGERTIAN NILAI MUTLAK

Nilai mutlak adalah suatu jarak antara bilangan tertentu dengan nol pada garis bilangan real. Karena jarak, maka nilainya selalu positif (tidak ada yang negatif). Sehingga nilai mutlak yaitu nilai yang selalu positif.

Konsep nilai mutlak digunakan pada Selisih bilangan selalu dianggap positif karena itu konsep nilai mutlah berlaku (digunakan) pada hitungan selilih bilangan.

Jarak suatu benda selalu dianggap positif karena konsep nilai mutlak digunakan pada hitungan jarak benda, Toleransi resistor (perubahan nilai resistansi), begitu juga dengan galat pengukuran juga menggunakan konsep nilai mutlak.

Contoh soal nilai mutlak

Rudi berjalan kekanan sejauh 10 langkah, kemudian kekiri 13 langkah, berapa jarak Rudi dengan titik semula?

Jawab: jarak Rudi dengan titik semula = I 10 - 13 I = I -3 I = 3 langkah

Meskipun hasil hitung negatif, karena nilai mutlak maka kita tulis positif.

Nilai x dari persamaan 3x + 2 = x + 2 adalah …

2

Jawab : 3x + 2 = (x + 2) x 2

3x + 2 = 2 x + 4

3x – 2x = 4 – 2

X = 2

Nilai x dari persamaan 4x – 6 = 10 adalah…

Jawab : 4x = 10 + 6

4x = 16

X = 16/4

X = 4

Nilai x dari persamaan 14 – 4x = 6x – 16 adalah …

Jawab : -4x -6x = -16 -14

-10x = – 30

X = -30/-10

X = 3

brainly.co.id