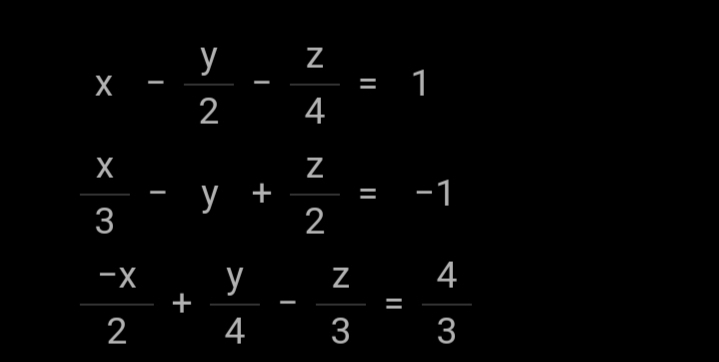Diena Naila Amalia
08 / X IPS 3
ax + by + cz = d
atau
a1x + b1y + c1z = d1
ex + fy + gz = h
a2x + b2y + c2z = d2
ix + jy + kz = l
a3x + b3y + c3z = d3
Dengan a, b, c, d, e, f, g, h, i, j, k, dan l atau a1, b1, c1, d1, a2, b2, c2, d2, a3, b3, c3, dan d3 merupakan bilangan-bilangan real.
Keterangan:
a, e, I, a1, a2, a3 = koefisien dari x
b, f, j, b1, b2, b3 = koefisien dari y
c, g, k, c1, c2, c3 = koefisien dari z
d, h, i, d1, d2, d3 = konstanta
x, y, z = variabel atau peubah
cara menentukan himpunan penyelesaian SPLTV berbentuk pecahan
Namun dalam soal-soal matematika yang berhubungan dengan sistem persamaan linear tiga variabel terkadang kita menemui SPLTV yang berbentuk pecahan seperti sistem persamaan linear berikut ini.
Lalu bagaimana menentukan himpunan penyelesaian SPLTV yang berbentuk pecahan tersebut? Caranya sangat mudah sekali, yaitu kita hanya perlu mengubah SPLTV pecahan menjadi bentuk baku atau bentuk umum seperti yang telah disebutkan di awal artikel. Setelah bentuk baku diperoleh, selanjutnya kita selesaiakan dengan menggunakan salah satu dari metode-metode berikut ini.
■ Metode subtitusi
■ Metode eliminasi
■ Metode gabungan atau campuran
■ Metode determinan
■ Metode invers matriks
Sebagai contoh, kita akan menentukan himpunan penyelesaian dari sistem persamaan linear tiga variabel yang berbentuk pecahan berikut ini.
Langkah-langkahnya adalah sebagai berikut.
■ Ubah persamaan yang memuat pecahan menjadi bentuk baku. Caranya adalah dengan mengalikan kedua ruas dengan KPK dari penyebut-penyebut pecahannya yaitu sebagai berikut.
Persamaan 1
KPK dari 1, 2 dan 4 adalah 4, oleh karena itu, agar menjadi bentuk baku, kita kalikan kedua ruas dengan angka 4 sehingga hasilnya adalah sebagai berikut.
4x – 2y – z = 4
Persamaan 2
KPK dari 3, 1, dan 2 adalah 6 oleh karena itu, agar menjadi bentuk baku, kita kalikan kedua ruas dengan angka 6 sehingga hasilnya adalah sebagai berikut.
2x – 6y + 3z = −6
Persamaan 3
KPK dari 2, 4 dan 3 adalah 12 oleh karena itu, agar menjadi bentuk baku, kita kalikan kedua ruas dengan angka 12 sehingga hasilnya adalah sebagai berikut.
−6x + 3y – 4z = 16
Dengan demikian, bentuk baku dari sistem persamaan linear tiga variabel bentuk pecahan di atas adalah sebagai berikut.
4x – 2y – z = 4 ……………….. Pers. (1)
2x – 6y + 3z = −6 ………….. Pers. (2)
−6x + 3y – 4z = 16 .……….. Pers. (3)
Baca Juga:
Kumpulan Contoh Soal SPLDV, SPLTV, SPLK, SPKK dan Jawabannya
Kumpulan Contoh Soal dan Jawaban SPLTV (Sistem Persamaan Linear Tiga Variabel)
5 Macam Metode Menentukan Penyelesaian SPLTV + Contoh Soal dan Pembahasan Bagian 3
■ Setelah bentuk SPLTV kita dapatkan, langkah selanjutnya adalah menentukan himpunan penyelesaian dari SPLTV tersebut dengan menggunakan salah satu dari 5 metode penyelesaian SPLTV di atas. Misalkan kita akan menggunakan metode campuran (eliminasi + subtitusi), sehingga penyelesaiannya adalah sebagai berikut.
#1 Metode Eliminasi (SPLTV)
Langkah pertama, kita tentukan variabel mana yang akan kita eliminasi terlebih dahulu. Untuk mempermudah, lihat variabel yang paling sederhana. Dari ketiga SPLTV di atas, variabel yang paling sederhana adalah y sehingga kita akan mengeliminasi y dulu. Untuk menghilangkan peubah z, maka kita harus menyamakan koefisien masing-masing y dari ketiga persamaan. Perhatikan cara berikut.
4x – 2y – z = 4 → koefisien y = –2
2x – 6y + 3z = −6 → koefisien y = –6
−6x + 3y – 4z = 16 → koefisien y = 3
Agar ketiga koefisien y sama (abaikan tanda), maka kita kalikan persamaan pertama dengan 3, persamaan kedua dengan 1, dan persamaan ketiga dengan 2. Sehingga hasilnya adalah sebagai berikut.
4x – 2y – z
=
4
|× 3|
→
12x – 6y – 3z
=
12
2x – 6y + 3z
=
−6
|× 1|
→
2x – 6y + 3z
=
−6
−6x + 3y – 4z
=
16
|× 2|
→
−12x + 6y – 8z
=
32
Setelah koefisien y ketiga persamaan sudah sama, maka langsung saja kita kurangkan atau jumlahkan persamaan pertama dengan persamaan kedua dan persamaan kedua dengan persamaan ketiga sedemikian rupa hingga variabel y hilang. Prosesnya seperti di bawah ini.
● Dari persamaan pertama dan kedua:
12x – 6y – 3z
=
12
2x – 6y + 3z
=
−6
−
10x − 6z
=
18
● Dari persamaan kedua dan ketiga:
2x – 6y + 3z
=
−6
−12x + 6y – 8z
=
32
+
−10x − 5z
=
26
Dengan demikian, kita peroleh SPLDV sebagai berikut.
10x – 6z = 18
−10x − 5z = 26
#2 Metode Subtitusi (SPLDV)
Dari SPLDV pertama, kita peroleh persamaan x sebagai berikut.
⇒ 10x – 6z = 18
⇒ 10x = 18 + 6z
Lalu kita subtitusikan persamaan y tersebut ke SPLDV kedua sebagai berikut.
⇒ −10x − 5z = 26
⇒ −(18 + 6z) − 5z = 26
⇒ −18 − 6z − 5z = 26
⇒ − 6z − 5z = 26 + 18
⇒ −11z = 44
⇒ z = −4
Kemudian, untuk menentukan nilai x, kita subtitusikan nilai z = −4 ke dalam salah satu SPLDV, misalnya persamaan 10x – 6z = 18 sehingga kita peroleh:
⇒ 10x – 6z = 18
⇒ 10x – 6(−4) = 18
⇒ 10x + 24 = 18
⇒ 10x = 18 – 24
⇒ 10x = –6
⇒ x = –6/10
⇒ x = –3/5
Langkah terakhir yaitu menentukan nilai y. Untuk menentukan nilai y, kita subtitusikan nilai x = –3/5 dan z = x = –4 ke dalam salah satu SPLTV di atas, misalnya persamaan 4x – 2y – z = 4 sehingga kita peroleh:
⇒ 4x – 2y – z = 4
⇒ 4(–3/5) – 2y – (–4) = 4
⇒ –12/5 – 2y + 4 = 4
⇒ –2y = 4 – 4 + 12/5
⇒ –2y = 12/5
⇒ y = –12/10
⇒ y = –6/5
⇒ y = –11/5
Dengan demikian kita peroleh nilai x = –3/5, y = –11/5 dan z = –4 sehingga himpunan penyelesaian SPLTV di atas adalah {(–3/, –11/5, –4)}.
SPLTV bentuk pecahan yang dibahas dalam artikel ini adalah posisi ketiga variabel (x, y, z) sebagai pembilang dalam pecahan. Lalu bagaimana cara menyelesaikan SPLTV bentuk pecahan yang variabelnya dijadikan sebagai penyebut pecahan? Perhatikan contoh SPLTV berikut.
Cara menentukan himpunan penyelesaian SPLTV pecahan dengan model seperti di atas dapat kalian jumpai dalam artikel tentang Contoh Soal + Pembahasan SPLTV Bentuk Pecahan.